Dadas duas retas r e s queremos encontrar a medida do ângulo formado por elas. Para tanto, usaremos o conceito de tangente (tg ou tan), para mais detalhes sugerimos que consulte a parte de Trigonometria.
Temos que r: y=mx+q e s: y=m'x+q'.
Sabemos que m e m' são coeficientes angulares das retas r e s, em relação ao eixo Ox. Como a é ângulo entre o eixo Ox e a reta s, bem como, b é ângulo entre o eixo Ox e a reta s, temos que
tg(a)=m' e tg(b)=m
então tg(c)=tg(a-b)
Das identidades trigonométricas temos que
colocando os valores das tangentes, teremos:
Se o valor encontrado para tg(c) estiver alistado em uma tabela trigonométrica de ângulos notáveis, será fácil descobrir o valor do ângulo c, caso contrário, teremos que fazer o inverso da tangente que é a arc tangente, como abaixo, mas, para tanto, provavelmente teremos que usar uma calculadora.
Exemplo:
Na figura abaixo temos a reta r que passa pelos pontos A(5,1) e B(4,4) e a reta s que passa pelos pontos C(2,1) e D(3,3), queremos encontrar a medida do ângulo c.
Inicialmente vamos calcular os coeficientes angulares m da reta r e m' da reta s.
Colocando os valores em nossa equação teremos:
Olhando para uma tabela trigonométrica de ângulos notáveis, encontraremos que tg(c)= -1 refere-se aos ângulos de 135° e -45°, portanto, c = 45° e seu suplementar c' = 135°.


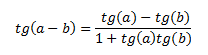






Nenhum comentário:
Postar um comentário